Calculadora de derivação



Insira a função a ser derivada.
Dicas: Enter sendo 3*x^2 ,
sendo 3/5 and
sendo (x+1)/(x-2x^4)



O que é uma derivada?

A derivada da função mostra em x qual inclinação do gráfico da função tem em x, ou seja, cuja inclinação há uma linha tangente no ponto (x|f(x))

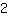
Exemplo: A normal da parábola f_f(x)=x^2 tem a linha tangente 2x-1 em (1|1), ou seja, inclinação 2. A derivada da normal da parábola em x=1 é igual a 2

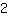
Qual a diferença entre derivada e derivada da função?

a derivada da função f´(x) de f(x) é a função que fornece a inclinação em x para cada x fornecido. Sigifica que: Para encontrar qual inclinação de f está em x, você só precisa inserir o x na função da derivada.

E como calcular a derivada?

Antes de encontrar as regras da diferenciação, é preciso calcular o quociente diferencial para cada ponto separadamente. Usando as regras de diferenciação, as coisas tornam-se simples: Primeiro, você calcula a derivada da funções potenciais. f_f(x)=x^n. É simples f_f'(x)=nx^(n-1). Outras regras possibilitam o cálculo da derivada de uma função polinomial arbitrária, porque é nada mais que a soma dos números e produtos das funções potenciais. Então você precisa dessas regras:
  • a regra fatorial f_f'(a*x)=a*f_f'(x)
  • e a regra da adição: A derivada igual
Para funções mais complicadas, serão necessárias outras regras:
  • a regra do produto: a derivada igual
  • a regra do quociente: a derivada igual
  • a regra da cadeia: a derivada igual

Por que encontrar a raíz da derivada?

As raízes da derivada são pontos importantes no gráfico. Nos pontos extremos máximos ou mínimos, a primeira derivada é zero. (Nota:) Não é porque a primeira derivada é zero que necessariamente é um ponto extremo. Confira a troca dos sinais para mais informações. Em um ponto extremo a segunda derivada é zero. Então você pode encontrar mais sobre sua função colocando a derivada igual a zero e resolver a equação.